首页 > 汇编语言 > 汇编语言基本概念简介
阅读:18,677
汇编语言布尔表达式(NOT、AND、OR)
布尔代数(boolean algebra)定义了一组操作,其值为真(true)或假(false)。它的发明者是十九世纪中叶的数学家乔治・布尔(George Boole)。
在数字计算机发明的早期,人们发现布尔代数可以用来描述数字电路的设计。同时,在计算机程序中,布尔表达式被用来表示逻辑操作。
一个布尔表达式(boolean expression)包括一个布尔运算符以及一个或多个操作数。每个布尔表达式都意味着一个为真或假的值。以下为运算符集合:
NOT 是一元运算符,其他运算符都是二元的。布尔表达式的操作数也可以是布尔表达式。示例如下:
真值表中,0 表示假,1 表示真。
当两个输入都是真时,输出才为真。这与 C++ 和 Java 的复合布尔表达式中的逻辑 AND 是相对应的。
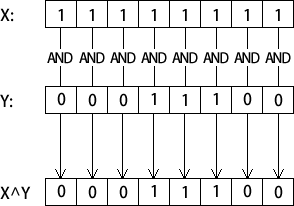
汇编语言中 AND 运算符是按位操作的。如下例所示,X 中的每一位都与 Y 中的相应位进行 AND 运算:
当两个输入都是假时,输出才为假。这个真值表与 C++ 和 Java 的复合布尔表达式中的逻辑 OR 对应。
OR 运算符也是按位操作。在下例中,X 的每一位与 Y 的对应位进行 OR 运算,结果为 1111 1100:

如下表所示,NOT 运算符具有最高优先级,然后是 AND 和 OR 运算符。可以使用括号来强制指定表达式的求值顺序:
示例 1:¬X∨Y
示例 2:X^¬Y
示例3: (Y^S)∨(X^¬S)
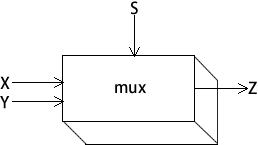
示例 3 的布尔函数描述了一个多路选择器(multiplexer),一种数字组件,利用一个选择位(S)在两个输出(X 和 Y)中选择一个。如果 S 为假,函数输出(Z)就和 X 相同;如果 S 为真,函数输出就和 Y 相同。下面是多路选择器的框图:
在数字计算机发明的早期,人们发现布尔代数可以用来描述数字电路的设计。同时,在计算机程序中,布尔表达式被用来表示逻辑操作。
一个布尔表达式(boolean expression)包括一个布尔运算符以及一个或多个操作数。每个布尔表达式都意味着一个为真或假的值。以下为运算符集合:
- 非(NOT):标记为 ¬ 或 ~ 或 '
- 与(AND):标记为^或 ·
- 或(OR):标记为 ∨ 或 +
NOT 是一元运算符,其他运算符都是二元的。布尔表达式的操作数也可以是布尔表达式。示例如下:
| 达式 | 说明 | 表达式 | 说明 |
|---|---|---|---|
| ¬X | NOT X | ¬X∨Y | (NOT X) OR Y |
| X^Y | X AND Y | ¬(X^Y) | NOT (X AND Y) |
| X∨Y | X OR Y | X^¬Y | X AND (NOT Y) |
NOT
NOT 运算符将布尔值取反。用数学符号书写为 ¬X,其中,X 是一个变量(或表达式),其值为真(T)或假(F)。下表列出了对变量 X 进行 NOT 运算后所有可能的输岀。 左边为输入,右边(阴影部分)为输出:| X | ¬X |
| F | T |
| T | F |
真值表中,0 表示假,1 表示真。
AND
布尔运算符 AND 需要两个操作数,用符号表示为 X ^ Y。下表列出了对变量 X 和 Y 进行 AND 运算后,所有可能的输出(阴影部分):| X | Y | X^Y |
| F | F | F |
| F | T | F |
| T | F | F |
| T | T | T |
当两个输入都是真时,输出才为真。这与 C++ 和 Java 的复合布尔表达式中的逻辑 AND 是相对应的。
汇编语言中 AND 运算符是按位操作的。如下例所示,X 中的每一位都与 Y 中的相应位进行 AND 运算:
X : 11111111
Y : 00011100
X ^ Y : 00011100

OR
布尔运算符 OR 需要两个操作数,用符号表示为 X∨Y。下表列出了对变量 X 和 Y 进行 OR 运算后,所有可能的输出:| X | Y | X∨Y |
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | T |
当两个输入都是假时,输出才为假。这个真值表与 C++ 和 Java 的复合布尔表达式中的逻辑 OR 对应。
OR 运算符也是按位操作。在下例中,X 的每一位与 Y 的对应位进行 OR 运算,结果为 1111 1100:
X : 11101100
Y : 00011100
X∨Y : 11111100

运算符优先级
运算符优先级原则(operator precedence rule)用于指示在多运算符表达式中,先执行哪个运算。在包含多运算符的布尔表达式中,优先级是非常重要的。如下表所示,NOT 运算符具有最高优先级,然后是 AND 和 OR 运算符。可以使用括号来强制指定表达式的求值顺序:
| 表达式 | 运算符顺序 |
| ¬X∨Y | NOT,然后 OR |
| ¬(X^Y) | OR,然后 NOT |
| X∨(X^Y) | AND,然后 OR |
布尔函数真值表
布尔函数(Boolean function)接收布尔输入,生成布尔输出。所有布尔函数都可以构造一个真值表来展示全部可能的输入和输出。下面的这些真值表都表示包含两个输入变量 X 和 Y 的布尔函数。右侧的阴影部分是函数输岀:示例 1:¬X∨Y
| X | ¬X | Y | ¬X∨Y |
| F | T | F | T |
| F | T | T | T |
| T | F | F | F |
| T | F | T | T |
示例 2:X^¬Y
| X | Y | ¬Y | X^¬Y |
| F | F | T | F |
| F | T | F | F |
| T | F | T | T |
| T | T | F | F |
示例3: (Y^S)∨(X^¬S)
| X | Y | S | Y^S | ¬S | X^¬S | (Y^S)∨(X^¬S) |
| F | F | F | F | T | F | F |
| F | T | F | F | T | F | F |
| T | F | F | F | T | T | T |
| T | T | F | F | T | T | T |
| F | F | T | F | F | F | F |
| F | T | T | T | F | F | T |
| T | F | T | F | F | F | F |
| T | T | T | T | F | F | T |
示例 3 的布尔函数描述了一个多路选择器(multiplexer),一种数字组件,利用一个选择位(S)在两个输出(X 和 Y)中选择一个。如果 S 为假,函数输出(Z)就和 X 相同;如果 S 为真,函数输出就和 Y 相同。下面是多路选择器的框图:
