首页 > 汇编语言 > 汇编语言基本概念简介
阅读:41,641
二进制加法运算
两个二进制整数相加时,是位对位处理的,从最低的一对位(右边)开始,依序将每一对位进行加法运算。两个二进制数字相加,有四种结果,如下所示:
1 与 1 相加的结果是二进制的 10(等于十进制的 2)。多出来的数字向更高位产生一个进位。如下图所示,两个二进制数 0000 0100 和 0000 0111 相加:
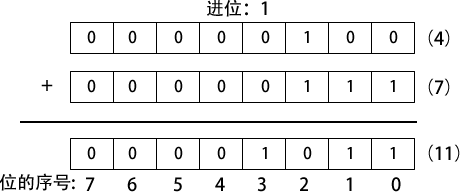
从两个数的最低位(位 0)开始,计算 0+1,得到底行对应位上的 1。然后计算次低位(位 1)。在位 2 上,计算 1+1,结果是 0,并产生一个进位 1。然后计算位 3,0+0,还要加上位 2 的进位,结果是 1。
其余的位都是 0。上图右边是等价的十进制数值加法(4 + 7 = 11),可以用于验证左边的二进制加法。
有些情况下,最高有效位会产生进位。这时,预留存储区的大小就显得很重要。比如,如果计算 1111 1111 加 0000 0001,就会在最高有效位之外产生一个 1,而和数的低 8 位则为全 0。
如果和数的存储大小最少有 9 位,那么就可以将和数表示为 1 0000 0000。但是,如果和数只能保存 8 位,那么它就等于 0000 0000,也就是计算结果的低 8 位。
| 0 + 0 = 0 | 0 + 1 = 1 |
| 1 + 0 = 1 | 1 + 1 = 10 |
1 与 1 相加的结果是二进制的 10(等于十进制的 2)。多出来的数字向更高位产生一个进位。如下图所示,两个二进制数 0000 0100 和 0000 0111 相加:

从两个数的最低位(位 0)开始,计算 0+1,得到底行对应位上的 1。然后计算次低位(位 1)。在位 2 上,计算 1+1,结果是 0,并产生一个进位 1。然后计算位 3,0+0,还要加上位 2 的进位,结果是 1。
其余的位都是 0。上图右边是等价的十进制数值加法(4 + 7 = 11),可以用于验证左边的二进制加法。
有些情况下,最高有效位会产生进位。这时,预留存储区的大小就显得很重要。比如,如果计算 1111 1111 加 0000 0001,就会在最高有效位之外产生一个 1,而和数的低 8 位则为全 0。
如果和数的存储大小最少有 9 位,那么就可以将和数表示为 1 0000 0000。但是,如果和数只能保存 8 位,那么它就等于 0000 0000,也就是计算结果的低 8 位。