首页 > 汇编语言 > 汇编语言基本概念简介
阅读:18,905
十六进制整数
大的二进制数读起来很麻烦,因此十六进制数字就提供了一种简便的方式来表示二进制数据。十六进制整数中的 1 个数字就表示了 4 位二进制位,两个十六进制数字就能表示一个字节。
一个十六进制数字表示的范围是十进制数 0 到 15,所以,用字母 A 到 F 来代表十进制数 10 到 15。
下表列出了每个 4 位二进制序列如何转换为十进制和十六进制数值。
下面的例子说明了二进制数 0001 0110 1010 0111 1001 0100 是如何与十六进制数 16A794 等价的。
下式计算了这个 整数的十进制值:
下图演示了第二个数转换的计算过程:
下表列出了 16 的幂从160 到167 的十进制数值。
表中,余数列的数字按照最后一行到第一行的顺序,组合为十六进制的结果。因此本例中,十六进制结果就表示为1A6。同样的算法也适用于《二进制整数》一节中的二进制整数。如果要将十进制数转换为其他进制数,就在计算时把除数(16)换成相应的基数。
一个十六进制数字表示的范围是十进制数 0 到 15,所以,用字母 A 到 F 来代表十进制数 10 到 15。
下表列出了每个 4 位二进制序列如何转换为十进制和十六进制数值。
| 二进制 | 十进制 | 十六进制 | 二进制 | 十进制 | 十六进制 |
|---|---|---|---|---|---|
| 0000 | 0 | 0 | 1000 | 8 | 8 |
| 0001 | 1 | 1 | 1001 | 9 | 9 |
| 0010 | 2 | 2 | 1010 | 10 | A |
| 0011 | 3 | 3 | 1011 | 11 | B |
| 0100 | 4 | 4 | 1100 | 12 | C |
| 0101 | 5 | 5 | 1101 | 13 | D |
| 0110 | 6 | 6 | 1110 | 14 | E |
| 0111 | 7 | 7 | 1111 | 15 | F |
下面的例子说明了二进制数 0001 0110 1010 0111 1001 0100 是如何与十六进制数 16A794 等价的。
| 1 | 6 | A | 7 | 9 | 4 |
| 0001 | 0110 | 1010 | 0111 | 1001 | 0100 |
无符号十六进制数到十进制的转换
十六进制数中,每一个数字位都代表了 16 的幂。这有助于计算一个十六进制整数的十进制值。假设用下标来对一个包含 4 个数字的十六进制数编号 D3D2D1D0。下式计算了这个 整数的十进制值:
dec = (D3 X 163) + (D2 X 162) + (D1 X 161) + (D0 x 160)
这个表达式可以推广到任意n位数的十六进制整数:dec = (Dn-1 X 16n-1)+ (Dn-2 x 16n-2)+…+ (D1 X 161)+ (D0 x 160)
一般情况下,可以通过公式把基数为B的任何n位整数转换为十进制数:dec = (D n-1 X Bn-1) + (Dn-2 X Bn-2) +…+ (D1 X B1) + (D0 x B0)。
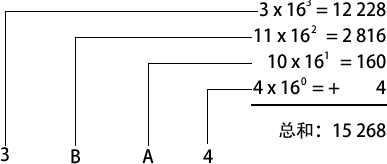
比如,十六进制数1234就等于(1 x 163) + (2 x 162) +(3X161) + (4x160),也就是十进制数 4660。同样,十六进制数 3BA4 等于(3 x 163)+(11 x 162)+(10 x 161)+( 4 x 160),也就是十进制数15 268。下图演示了第二个数转换的计算过程:

下表列出了 16 的幂从160 到167 的十进制数值。
| 16n | 十进制值 | 16n | 十进制值 |
|---|---|---|---|
| 160 | 1 | 164 | 65 536 |
| 161 | 16 | 165 | 1 048 576 |
| 162 | 256 | 166 | 16 777 216 |
| 163 | 4096 | 167 | 268 435 456 |
无符号十进制数到十六进制的转换
无符号十进制整数转换到十六进制数的过程是,把这个十进制数反复除以16,每次取余数作为一个十六进制数字。例如,下表列出了十进制数 422 转换为十六进制的步骤:| 除法 | 商 | 余数 |
|---|---|---|
| 422/16 | 26 | 6 |
| 26/16 | 1 | A |
| 1/16 | 0 | 1 |
表中,余数列的数字按照最后一行到第一行的顺序,组合为十六进制的结果。因此本例中,十六进制结果就表示为1A6。同样的算法也适用于《二进制整数》一节中的二进制整数。如果要将十进制数转换为其他进制数,就在计算时把除数(16)换成相应的基数。