首页 > 汇编语言 > 汇编语言基本概念简介
阅读:45,143
补码及进制转换
有符号二进制整数有正数和负数。在 x86 处理器中,MSB 表示的是符号位:0 表示正数,1 表示负数。下图展示了 8 位的正数和负数:
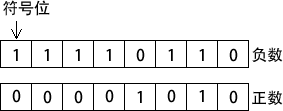
补码表示法对处理器设计者来说很有用,因为有了它就不需要用两套独立的电路来处理加法和减法。例如,如果表达式为 A-B,则处理器就可以很方便地将其转换为加法表达式:A+(-B)。
将一个二进制整数按位取反(求补)再加 1,就形成了它的补码。以 8 位二进制数 0000 0001 为例,求其补码为 1111 1111,过程如下所示:
1111 1111 是 -1 的补码。补码操作是可逆的,因此,11111111 的补码就是 0000 0001。
例如,有符号二进制数 1111 0000 的最高有效位是 1,这意味着它是一个负数,首先要求它的补码,然后再将结果转换为十进制。过程如下所示:
由于初始值(1111 0000)是负数,因此其十进制数值为 -16。
比如,十进制数 -43 转换为二进制的过程为:
1) 无符号数 43 的二进制表示为 0010 1011。
2) 由于初始数值是负数,因此,求出 0010 1011 的补码 1101 0101 这就是十进制数 -43 的二进制表示。
通过检查十六进制数的最高有效(最高)位,就可以知道该数是正数还是负数。如果最高位 ≥ 8,该数是负数;如果最高位 ≤ 7,该数是正数。比如,十六进制数 8A20 是负数,而 7FD9 是正数。

补码表示
负整数用补码(two`s-complement)表示时,使用的数学原理是:一个整数的补码是其加法逆元。(如果将一个数与其加法逆元相加,结果为 0。)补码表示法对处理器设计者来说很有用,因为有了它就不需要用两套独立的电路来处理加法和减法。例如,如果表达式为 A-B,则处理器就可以很方便地将其转换为加法表达式:A+(-B)。
将一个二进制整数按位取反(求补)再加 1,就形成了它的补码。以 8 位二进制数 0000 0001 为例,求其补码为 1111 1111,过程如下所示:
| 初始值 | 00000001 |
| 第一步:按位取反 | 11111110 |
| 第二步:将上一步得到的结果加 1 |
11111110 +00000001 |
| 和值:补码表示 | 11111111 |
1111 1111 是 -1 的补码。补码操作是可逆的,因此,11111111 的补码就是 0000 0001。
十六进制数的补码
将一个十六进制整数按位取反并加 1,就生成了它的补码。一个简单的十六进制数字取反方法就是用 15 减去该数字。下面是一些十六进制数求补码的例子:
6A3D --> 95C2 + 1 --> 95C3
95C3 --> 6A3C + 1 --> 6A3D
有符号二进制数到十进制的转换
用下面的算法计算一个有符号二进制整数的十进制数值:- 如果最高位是 1,则该数是补码。再次对其求补,得到其正数值。然后把这个数值看作是一个无符号二进制整数,并求它的十进制数值。
- 如果最高位是 0,就将其视为无符号二进制整数,并转换为十进制数。
例如,有符号二进制数 1111 0000 的最高有效位是 1,这意味着它是一个负数,首先要求它的补码,然后再将结果转换为十进制。过程如下所示:
| 初始值 | 11110000 |
| 第一步:按位取反 | 00001111 |
| 第二步:将上一步得到的结果加 1 |
00001111 + 1 |
| 第三步:生成补码 | 00010000 |
| 第四步:转换为十进制 | 16 |
由于初始值(1111 0000)是负数,因此其十进制数值为 -16。
有符号十进制数到二进制的转换
有符号十进制整数转换为二进制的步骤如下:- 把十进制整数的绝对值转换为二进制数。
- 如果初始十进制数是负数,则在第 1 步的基础上,求该二进制数的补码。
比如,十进制数 -43 转换为二进制的过程为:
1) 无符号数 43 的二进制表示为 0010 1011。
2) 由于初始数值是负数,因此,求出 0010 1011 的补码 1101 0101 这就是十进制数 -43 的二进制表示。
有符号十进制数到十六进制的转换
有符号十进制整数转换为十六进制的步骤如下:- 把十进制整数的绝对值转换为十六进制数。
- 如果初始十进制数是负数,则在第 1 步的基础上,求该十六进制数的补码。
有符号十六进制数到十进制的转换
有符号十六进制整数转换为十进制的步骤如下:- 如果十六进制整数是负数,求其补码,否则保持该数不变。
- 把第 1 步得到的整数转换为十进制。如果初始值是负数,则在该十进制整数的前面加负号。
通过检查十六进制数的最高有效(最高)位,就可以知道该数是正数还是负数。如果最高位 ≥ 8,该数是负数;如果最高位 ≤ 7,该数是正数。比如,十六进制数 8A20 是负数,而 7FD9 是正数。
最大值和最小值
n 位有符号整数只用 n-1 来表示该数的范围。下表列出了有符号单字节、字、双字、四字和八字的最大值与最小值。| 类型 | 范围 | 存储位数 | 类型 | 范围 | 存储位数 |
|---|---|---|---|---|---|
| 有符号字节 | -27 到 +27-1 | 8 | 有符号四字 | -263 到 +263-1 | 64 |
| 有符号字 | -215 到 +215-1 | 16 | 有符号八字 | -2127 到 +2127-1 | 128 |
| 有符号双字 | -231 到 +231-1 | 32 |